Travail d'une force
Le travail d'une force est l'énergie (en Joule) que cette force apporte au système lors d'un déplacement.
On note :

\Large \boxed{W_{AB}(\vec{F})=\vec{F}.\overrightarrow{AB}=F \times AB \times \cos(\alpha)}

W_{AB} en J
F en N
AB en m
\alpha en degré ou radian
- Le travail de la force est moteur si la force "aide l'objet à se déplacer", c'est-à-dire si l'angle est compris entre 0° et 90°. Le travail est positif.
- Le travail de la force est résistant si la force "empêche l'objet de se déplacer", c'est-à-dire si l'angle est compris entre 90° et 180°. Le travail est négatif.
Remarque :
Une force perpendiculaire au déplacement ne travaille pas (le travail est nul).
Travail de forces particulières
Pour certaines forces, l'expression du travail est toujours la même. Il pourra donc être utile de les connaître.
Poids
Le poids est une force verticale dirigée vers la bas. Elle ne travaille donc que sur la direction verticale. Le travail du poids ne dépend pas du chemin suivi mais uniquement de la différence d'altitude entre le point de départ et le point d'arrivée notée h.
Le travail est positif si l'objet descend, négatif s'il monte.
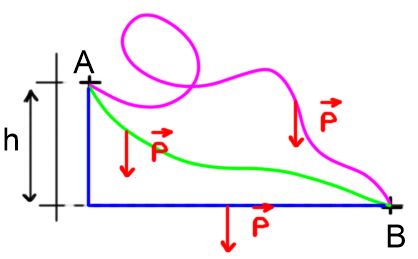
Le travail est le même sur les trois trajets
\boxed {\Large W_{AB}(\vec{P})=\pm m \times g \times h}

W_{AB} en J
m en kg
g = 9,81 N.kg-1
h en m
Réaction du support
La réaction du support est toujours perpendiculaire au déplacement.
Elle ne travaille jamais.
\boxed {\Large W_{AB}(\vec{R})=0}

Forces de frottement
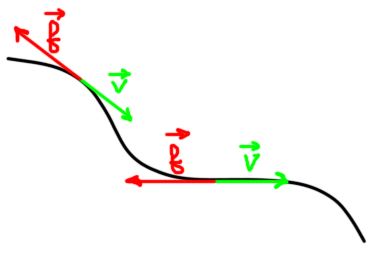
Les forces de frottement sont tangentes et opposées au mouvement.
Leur travail est toujours négatif, et elles travaillent totalement durant tout le trajet
\boxed {\Large W_{AB}(\vec{f})=- \, f \times \overset{\frown}{AB}}
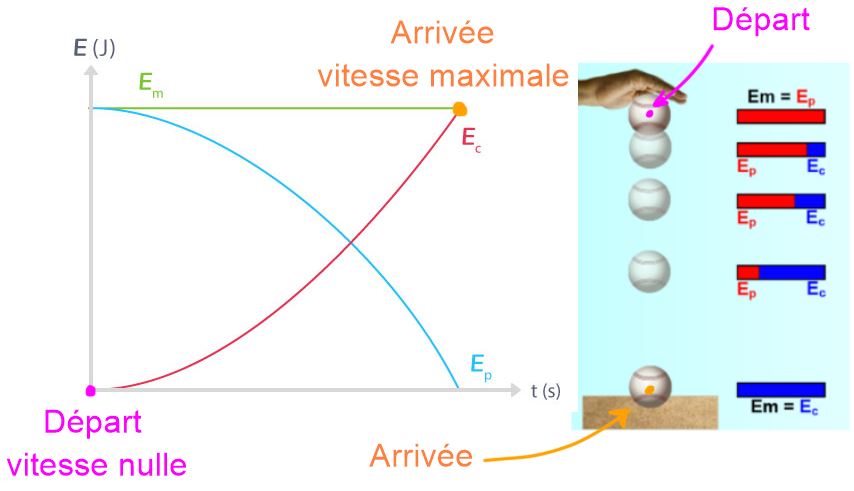
Énergie d'un objet
Un objet possède différentes formes d'énergie liées à sa position et son mouvement.
Énergie cinétique
C'est l'énergie que possède un objet lorsqu'il se déplace. Plus il va vite plus son énergie cinétique est grande.
\boxed {\Large E_C=\frac{1}{2} \times m \times v^2}

E_C en J
m en kg
V en m.s-1
Énergie potentielle
C'est l'énergie que pourrait libérer l'objet s'il se mettait en mouvement.
Un objet posé sur la table pourrait libérer de l'énergie s'il quittait la table puisque le poids l'entrainerai vers le bas. Cette énergie potentielle liée au poids est appelée énergie potentielle de pesanteur, et elle est égale au travail si l'objet se déplaçait.
\boxed {\Large E_{PP}= m \times g \times h}
avec h la hauteur entre l'objet et l'origine des altitudes.
On pourrait de la même manière calculer l'énergie potentielle que possède un ressort comprimé. Il faudrait calculer le travail que le ressort donnerait s'il se détendait (exemple : ressort de carabine à air comprimé).
Énergie mécanique
C'est l'énergie totale que possède un objet du point de vue mécanique :
\boxed {\Large E_m= E_{C}+E_{P}}
Variation d'énergie
Énergie cinétique
La vitesse d'un objet varie s'il perd ou gagne de l'énergie.
La variation d'énergie cinétique entre A et B est égale à la somme des travaux des forces agissant sur lui au cours du déplacement.
\boxed {\Large E_{C}(B)-E_{C}(A)= \sum W_{AB}(\vec{F})}
Énergie mécanique
Elle reste constante si l'objet ne subit pas de frottements.
C'est la cas par exemple de la chute libre (seul le poids agit).
Lors de sa chute, l'objet perd de l'énergie potentielle (puisqu'il descend) et la transforme intégralement en énergie cinétique (il prend de la vitesse), mais globalement son énergie mécanique reste constante.