Référentiel
Un référentiel est un objet par rapport auquel on va étudier le mouvement de notre système.
Afin de pouvoir utiliser les lois de la physique (lois de Newton notamment) le référentiel doit être choisi précisément :
- TERRESTRE : cas des mouvements de courte durée (lancé de balle, déplacement d'une voiture...)
- GEOCENTRIQUE : cas des mouvements de plusieurs heures (satellite, Lune...)
- HELIOCENTRIQUE : cas des mouvements des planètes
Pour les mouvements de la vie de tous les jours le référentiel TERRESTRE sera utilisé (c'est-à-dire le sol).
Trajectoire, translation et rotation
Au lycée l'étude du mouvement d'un objet se résume à celle de son centre de masse. On considèrera donc le système comme ponctuel.
Trajectoire
La trajectoire d'un objet est l'ensemble des positions qu'il occupe au cours du temps.

Translation
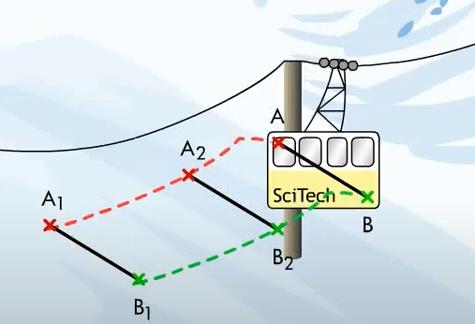
Dans un mouvement de translation tout segment de l'objet reste parallèle à lui-même au cours du mouvement.
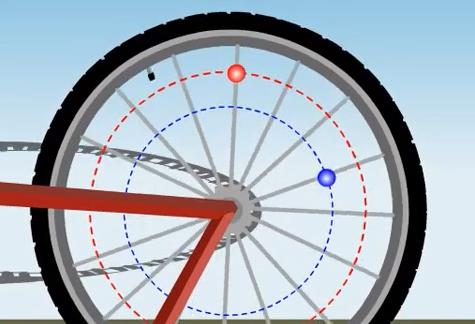
Rotation
Dans un mouvement de rotation tous les points de l'objet décrivent des cercles de même centre.
Vitesse
Dans le programme de STI2D on n'étudiera que des mouvements rectilignes. La vitesse sera donc étudiée dans une seule direction, il n'y a donc pas d'intérêt à représenter la vitesse comme un vecteur, seule sa valeur nous intéresse (ce qui va grandement simplifier le problème).
Vitesse moyenne
On sait depuis la troisième calculer une vitesse moyenne. Pour cela il faut faire le quotient de la distance parcourue par le temps mis pour la parcourir.
\boxed {\Large V_{moy}=\frac{d}{t}}

V en m.s-1
d = m
t en s
Rappel : on passe des km/h aux m/s en DIVISANT par 3,6
Vitesse instantanée
On peut assimiler une vitesse instantanée à une vitesse moyenne sur une durée extrêmement faible.
\Large v(t)=\lim\limits_{\Delta t \rightarrow 0} \frac{x(t+\Delta t)-x(t)}{\Delta t}
Cette limite est définie en mathématiques comme la dérivée d'où l'écriture :
\boxed {\Large v(t)=\frac{d \, x(t)}{dt}}
Accélération
De même que la vitesse représente la variation de la position du système, l'accélération va représenter la variation de la vitesse.
On va appliquer le même raisonnement que pour la vitesse (variation sur une durée très faible) ce qui donne l'expression de l'accélération :
\boxed {\Large a(t)=\frac{d \, v(t)}{dt}}

