Des vecteurs force à l'accélération
Un skieur de masse 80kg se trouve sur un remonte pente au moment du départ. La pente forme un angle a=35° avec l'horizontale.
Le sol exerce sur lui une force qui l’empêche de s'enfoncer dans la neige de valeur R=655N et la perche le tire dans la direction de la pente avec une valeur de T=600N.
Questions
- Représenter les forces exercées sur le skieur (supposé ponctuel) avec une échelle de 1cm pour 200N.
- En déduire le vecteur "résultante des forces.
- Donner la direction et le sens du vecteur accélération.
- En déduire que le skieur accélère
- Donner la valeur du vecteur accélération.
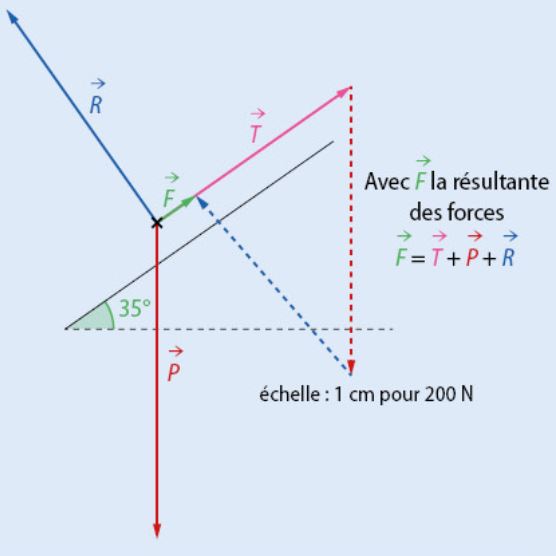
On commence par tracer les trois vecteurs force connus (poids, réaction du sol et traction de la perche) en utilisant l'échelle fournie.
On trace ensuite la résultante des forces dont on peut trouver la valeur grâce à l'échelle.
On applique alors la deuxième loi de Newton qui nous permet de dire que la valeur de l'accélération est égale à la valeur de la résultante des forces divisée par la masse de l'objet.
Théorème de l'énergie cinétique
Un cycliste veut estimer la valeur des forces de frottement lors d'un freinage d'urgence. Il se lance donc à une vitesse de 30km/h sur une piste d'entrainement et essaye de s'arrêter le plus rapidement possible. Il parvient à s'arrêter en 12m.
Le cycliste et son vélo ont une masse de 70kg, on considèrera que l'intensité de pesanteur vaut 10N/kg.
- Faire un bilan des forces qui s'exercent sur le vélo lors du freinage. On considèrera que les forces de frottements sont constantes.
- Quelles forcent "travaillent" durant le freinage ?
- En utilisant le théorème de l'énergie cinétique trouver la valeur des forces de frottement.
