La tension électrique dans les installations domestiques est alternative sinusoïdale de valeur efficace 230V et de fréquence 50Hz.
Les installations domestiques ne sont pas constituées uniquement d'appareils résistifs, mais aussi de bobines et/ou condensateurs qui induisent un déphasage entre la tension et l'intensité.
On se propose d'étudier ce phénomène et ses conséquences sur la puissance.
Tension sinusoïdale et déphasage
Modéliser une tension sinusoïdale
Expression mathématique d'une grandeur sinusoïdale
Une tension sinusoïdale peut être décrite par une fonction mathématique :
u(t)=U_{MAX} \times \sin(\omega.t) avec \omega=2.\pi.f
- \omega s'exprime en rad/s
- f s'exprime en Hz
Le générateur sera un générateur 6V alternatif, la tension u(t) est la tension de sortie de ce générateur.
Questions :
- Mesurer la valeur maximale, la valeur efficace, la période et la fréquence de la tension à la sortie du générateur.
- En déduire l'expression mathématique de la tension u(t).
Mesures
Grâce au logiciel "Mesure Electrique" on détermine la tension maximale et la période.
- U_{MAX} = = 8,96 V
- T = 20 ms
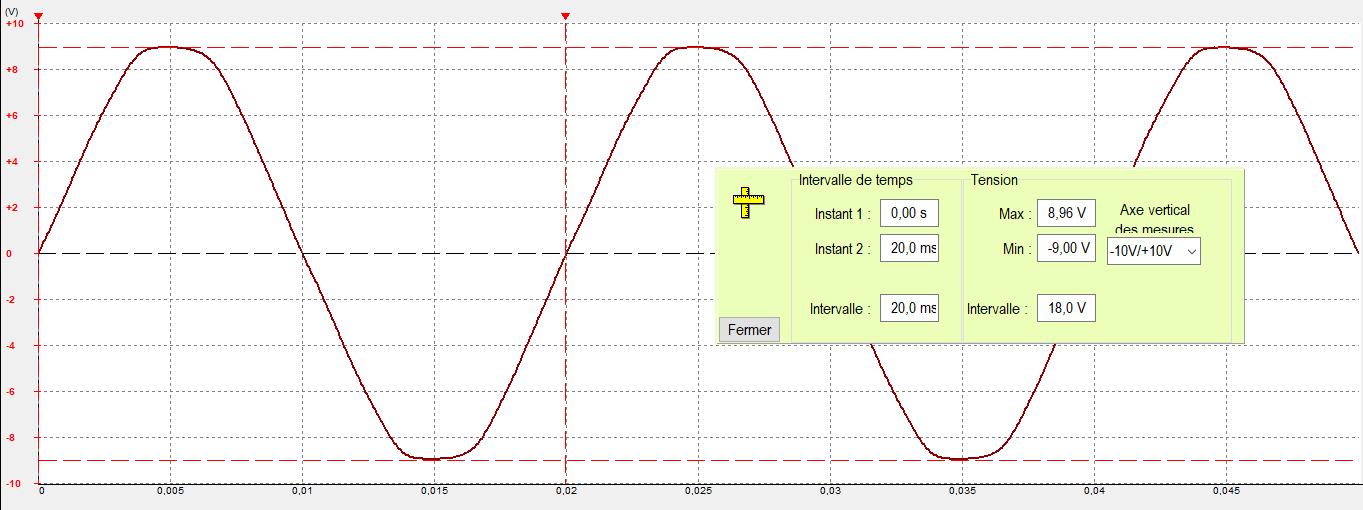
On peut alors calculer la fréquence et la valeur efficace de la tension :
- f = 1 / T avec T en s soit f = 1 / 20.10-3 = 50 Hz
- U_{EFF} = \frac{U_{MAX}}{\sqrt{2}} = \frac{8,96}{\sqrt{2}} = 6,3 V
Remarque : on aurait pu trouver la valeur efficace de la tension directement grâce au VOLTMÈTRE.
Expression mathématique de u(t)
D'après le document "Expression mathématique d'une grandeur sinusoïdale" on sait que la tension peut s'exprimer :
u(t)=U_{MAX} \times \sin(\omega.t) avec \omega=2.\pi.f
On en déduit que u(t)=8,96 \times \sin(314 \times t)
Notion de déphasage
Déphasage dans une installation
Dans une installation électrique certains composants sont purement résistif (radiateur, fils, four…). Si on observe la tension et l’intensité dans le circuit, ces deux grandeurs sont en phase.

En réalité certains appareils utilisent des composants non résistifs :
- certains inductifs (on parle de bobines) : les transformateurs, moteurs, télérupteurs…
- d'autres capacitifs (on parle de condensateurs)
La conséquence est que la tension en l’intensité ne sont plus en phase dans le circuit : cela veut dire que lorsqu’une des deux grandeurs est maximale l’autre ne l’est pas. La tension et l’intensité sont déphasées.
CALCULER UN DÉPHASAGE : https://www.youtube.com/watch?v=OasGP2u4SJo

Modélisation d'un moteur alternatif
On modélise un moteur alternatif par une résistance (R = 220 Ω) montée en série avec une bobine. L'alimentation sera un générateur de tension sinusoïdale de 6V.
Le wattmètre permettra d'obtenir les valeurs efficaces, la puissance active et le facteur de puissance.

Réaliser le montage de façon à observer les tensions u(t) et uR(t) .
Une fois le montage vérifié par le professeur observer u(t) et uR(t) grâce au logiciel "Mesure électrique".
Remarque : la masse de la carte SYSAM sera prise entre le générateur et la résistance.
- u(t) : voie EA0
- uR(t) : voie EA1
- Durée de mesure : 50 ms
Questions :
- Quel lien existe-t-il entre la tension aux bornes de la résistance uR(t) et l'intensité i(t) dans le circuit ?
- Imprimer les courbes obtenues et les sauvegarder le fichier au format rw3.
- En déduire la valeur du déphasage φ entre u(t) et i(t)

Fichier regressi (clic droit "enregistrer le lien sous...") : tension et intensité dans un moteur
Lien entre uR(t) et i(t)
On sait qu'aux bornes d'une résistance u et i sont proportionnels et suivent la loi d'ohm : u(t) = R x i(t)
Il en résulte qu'aux bornes d'une résistance la tension et l'intensité sont en phase.
Observer i(t) revient à observer uR(t).
Ci-dessous les courbes u(t) et uR(t) avec le déphasage représenté.

On obtient donc les valeurs suivantes :
- UMAX = 9,4 V
- UR(MAX) = 5,3 V
- Le déphasage correspond à une longueur D = 2,3 cm sur les courbes imprimées et la période L = 15,3 cm.
Détermination du déphasage
D'après ce qu'on vient de dire on peut mesurer le déphasage entre u et uR.
On peut dire :
\phi = \frac{2 \pi \times 2,3}{15,3}=0,944 rad
ou
\phi = \frac{360 \times 2,3}{15,3}=54°
Puissance active
Puissance active et valeurs instantanées
La puissance instantanée est définie par : p(t) = u(t) x i(t). La puissance active est la valeur moyenne de cette puissance instantanée.
Une fois qu'on aura représenté p(t) il suffira donc d'en calculer la valeur moyenne.
Questions :
- Importer les mesures précédentes dans Regressi et créer les grandeurs i(t) et p(t)
- Créer la grandeur p(t) puissance instantanée.
- Calculer la valeur moyenne de cette puissance et la comparer au produit UEFF x IEFF
- Mesurer la puissance active grâce au wattmètre et conclure.
Création de la grandeur i(t)
On détermine la grandeur i(t) à partir de uR(t) mesuré précédemment : i(t) = uR(t) / R
En rouge ci-dessous la tension u(t) du générateur et en bleu l'intensité i(t) dans le circuit.

Création de la grandeur p(t)
On crée maintenant p(t) = u(t) x i(t) puis on en calcule la valeur moyenne qui afin d'obtenir la puissance active.
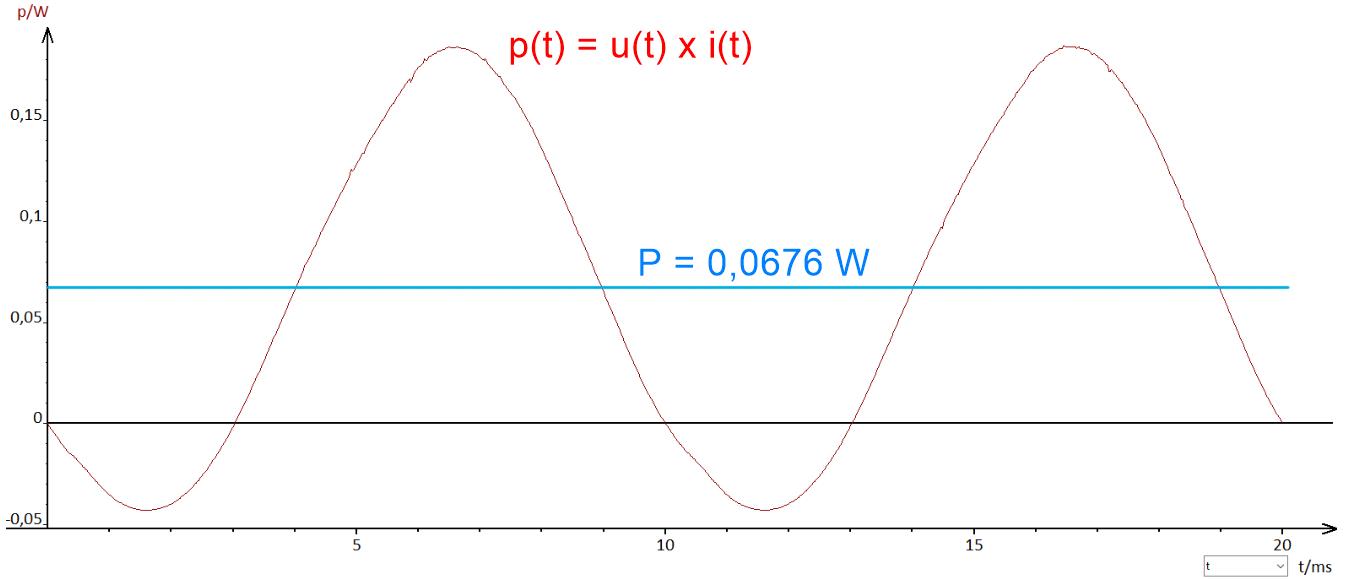
On obtient alors une valeur de puissance active égale à 0,0676 W.
Les valeurs efficaces de tension et d'intensité (obtenues directement avec le wattmètre ou par le calcul à partir des courbes u(t) et i(t) sont :
- UEFF = 6,63 V
- IEFF = 17 mA
Le calcul de UEFF x IEFF = 6,63 x 0,017 = 0,11 W ce qui ne correspond pas à la puissance active trouvée précédemment (0,0676 W).
Le produit UEFF x IEFF ne donne donc pas la puissance active !
Puissance active et valeurs efficaces
La puissance active en régime sinusoïdal est définie par : P= UEFF x IEFF cosφ
Questions :
- Calculer P=U.I.cosφ.
- Comparer la valeur à celle donnée par le wattmètre et conclure.
Calcul de la puissance active à partir du déphasage
Les valeurs efficaces de la tension et de l'intensité ont été trouvées précédemment.
- UEFF = 6,63 V
- IEFF = 17 mA
Le déphasage a été déterminé en début de TP :
- φ = 0,944 rad
On calcule la puissance active : P = UEFF x IEFF x cos(φ) = 6,63 x 0,017 x cos (0,944) = 0,066 W
On retrouve une valeur très proche de celle donnée par le wattmètre.
Résumé
Puissance apparente : P = UEFF x IEFF
Facteur de puissance : k = cos(φ) = P / S
Puissance active : P = UEFF x IEFF x cos(φ)
