Notion de déphasage
Lorsqu'un montage ne contient pas que des résistances (en plus des générateurs) un phénomène appelé déphasage apparaît.
On observe alors que la tension et l'intensité ne sont pas maximum (ou nuls) en même temps.
Le déphasage peut :
- se mesurer (avec un wattmètre par exemple)
- se calculer à partir des courbes u(t) et i(t) :
Exemple :
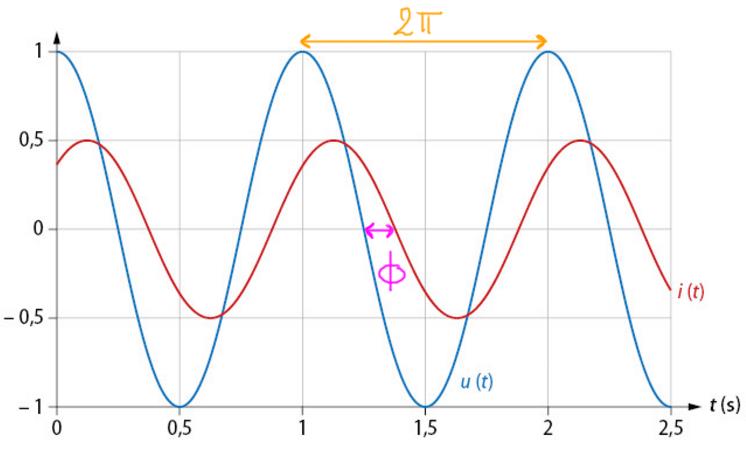
Sur la courbe ci-contre on mesure la "longueur" L qui représente une période (soit une rotation de 360° ou 2π rad). On mesure ensuite la longueur D qui représente le déphasage ϕ.
\boxed {\Large {\phi = 2\pi \times \frac{D}{L}}}
Puissance active
Définition
La puissance active est la moyenne des puissances instantanées.
Si on dispose de la courbe p(t) il est alors aisé de trouver la valeur moyenne.
Exemple : ci-contre la courbe p(t). La puissance active est la puissance moyenne de p(t) donc ici on trouve P = 100 W

Calculer la puissance active
Si on ne dispose pas de la courbe p(t) on peut calculer la puissance active. Deux cas se présentent alors :
Montage purement résistif
Les récepteurs ne sont que des résistances, la tension et l'intensité sont en phase.

\boxed {\Large{P = U \times I }}
Montage non résistif
Le montage peut contenir des bobines et/ou des condensateurs. La tension et l'intensité sont alors déphasés.

\boxed {\Large{P = U \times I \times \cos(\phi)}}

U et I sont des valeurs efficaces !
Puissance apparente et facteur de puissance
La puissance apparente S permet de dimensionner une installation (savoir quelle pourrait être la plus grande puissance consommée par l'installation). Elle s'exprime en V.A (dans ce cas précis on ne peut pas dire que ce sont des Watt car la puissance apparente est un "artifice de calcul" mais n'a pas de réalité physique)
\boxed {\Large{S = U \times I}}
Le facteur de puissance permet de relier les puissances actives et apparentes :
\boxed {\Large{k = \frac{P}{S} = \cos(\phi)}}
Exemple : une installation électrique fonctionnant sous 400 V permet d'alimenter un atelier dont la puissance active vaut P = 5,4 kW et le facteur de puissance k = 0,92.
Calculer l'intensité efficace qui va que doit fournir l'installation.
S = U \times I et k = \frac{P}{S} = \cos(\phi)
On peut calculer la puissance apparente : S = \frac{P}{k} = \frac{5,4}{0,92} = 5,9 kV.A
On en déduit l'intensité : I = \frac{S}{U} = \frac{5,9.10^3}{400} = 15 A
