Ordres de grandeur des puissances
Associer à chaque appareil la puissance produite ou consommée.
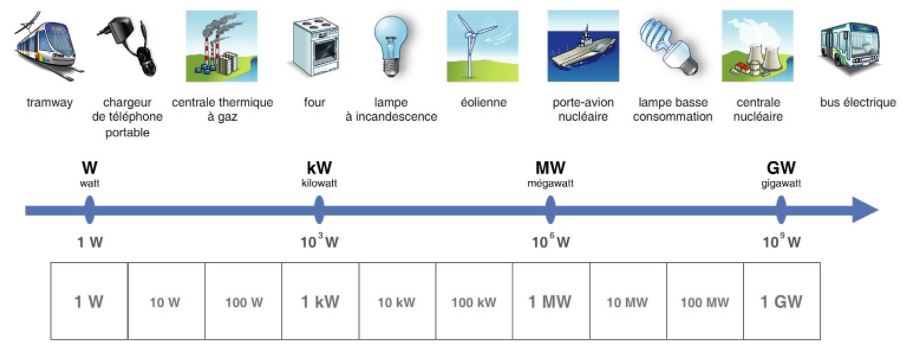

Notion de puissances
Pour chaque enregistrement p(t) ci-dessus dont l’axe des ordonnées est gradué en W donner les valeurs maximales, minimales et moyennes de la puissance.

Les courbes sont ici périodiques. Leur forme fait que si on fait la moyenne entre les valeurs minimales et maximales on trouve exactement la puissance moyenne.
1) Minimum : 200 W Maximum : 400 W Moyenne : 300 W
2) Minimum : 0,5 W Maximum : 1,5 W Moyenne : 1,0 W
3) Minimum : 250 W Maximum : 450 W Moyenne : 350 W
ATTENTION : dans certains cas c'est plus compliqué, il ne suffit pas de faire la moyenne mais il faut réellement calculer l'énergie consommée sur une période puis diviser par le temps. Ci dessous la puissance moyenne vaut :
P = (1,5 kW x 1,5 s + 0,5 kW x 0,5 s) / 2 s = 1,37 kW

De l'énergie à la puissance
Ci-contre le relevé de consommation d’une habitation.
A quel moment n’y a-t-il pas de consommation dans l'habitation ?
Représenter sur le graphe la courbe p(t)
Peut-on savoir, sans calcul, à quel moment de la journée il y a un pic de consommation.
Calculer la puissance moyenne sur une journée

1) Entre 8 et 16 heures l'énergie consommée ne change pas. La pente de la courbe e(t) (et donc la puissance) est nulle.
2) On calcule la pente des différents intervalles :
* Portion 1 : P=5/6=0,83 kW
* Portion 2 : P=(20-5)/2=7,5 kW
* Portion 3 : P=0 kW
* Portion 4 : P=(35-20)/2=7,5 kW
* Portion 5 : P=(40-35)/6=0,83 kW
On choisit ensuite une échelle de puissance (en rouge sur le graphe) et positionne les valeurs (sur le graphe ci dessous je l'ai fait de façon approximative).

3) Le pic de consommation correspond à la plus forte puissance, donc pente de la courbe e(t). Ce sont ici les intervalles 6-8 h et 16-18 h.
4) Pour avoir la puissance moyenne sur une journée il suffit de diviser l'énergie consommée par la durée : P = 40 kW.h / 24 h = 1,7 kW
En voiture

1) La puissance de la climatisation ne dépend pas de la vitesse, celle du roulement est proportionnelle et ceux de l’air proportionnels à la vitesse au cube. entre 130 et 100 la vitesse a été multipliée par 1,3 d’où :
P_{clim}=1 kW
P_{roulement}=3 kW \times 1,3 = 3,9 kW
P_{air}=7 kW \times 1,3^3= 15,4 kW
On voit qu’à 130km/h la voiture consomme 20,3 kW soit presque le double de ce qu’elle consomme à 100km/h !
2) Il suffit de diviser l’énergie consommée par le temps soit : P = 11,6 kW / 2 = 5,8 kW
3) On voit bien la grande puissance consommée entre 30 minutes et 1H15 sur diagramme bâton ci-dessous

4) Pour une vitesse de 100km/h la puissance consommée vaut 11 kW. Cela correspond aux pics de la courbe entre 30 minutes et 1H15.
Un vélo électrique
L’autonomie d’un vélo électrique peut varier de 20 à 80 km en moyenne selon le type de batterie, mais aussi suivant le type de parcours réalisé.
Capacité de la batterie : réservoir d’énergie du vélo, la batterie a une capacité exprimée en Wh. Plus elle sera élevée, meilleure sera l’autonomie. Les batteries des modèles d’entrée de gamme ont une capacité de 300-400 Wh contre 600-800 Wh pour les batteries haut de gamme. Une batterie de 36 V et 14 Ah a une capacité de 14 V x 36 Ah = 504 Wh.
Niveau d'assistance : le niveau d’assistance choisi a un impact sur l’autonomie. En montée une assistance importante sera nécessaire mais consomme beaucoup d’énergie. Il faut donc veiller à diminuer l’assistance en terrain plat pour gagner en autonomie.
Types de parcours : Avant de se lancer dans un périple, il faudra analyser sa topographie. En effet, plus il y aura de dénivelé moins vous pourrez parcourir de distance.
Poids de l’utilisateur : Les autonomies annoncées par les fabricants prennent en compte un utilisateur dont la masse est voisine de 60 kg. Pour un vélo de 22 kg cela fera une masse totale à transporter de 82 kg. Une personne de 80 kg devra donc prévoir de consommer 20% de plus pour un même trajet et donc de réduire l’autonomie d’autant.
- La batterie du vélo fait 400 W.h. Quelle énergie (en J) peut-elle fournir ?
- Sur terrain plat, l'autonomie vaut 40 km pour une vitesse de 20 km/h. Quelle est la durée d’utilisation ?
- La puissance du moteur est de 250 W. En supposant qu’il a fonctionné sur le trajet précédent avec une puissance de 180W, calculer l’énergie apportée par la batterie. A quoi a servi cette énergie pour le cycliste ?
- Déduire de la question précédente la valeur des forces de frottement.
- Un cycliste fait un parcours d’un dénivelé de 500m. Estimer la distance sur laquelle il pourra disposer d’une assistance électrique si on suppose qu’il a une vitesse de 15km/h.

1) On passe des W.h aux J en multipliant 3600 donc E = 1,44 MJ
2) Le cycliste peut parcourir 40 km à 20 km/h donc t = d / V = 40 (km) / 20 (km/h) = 2 h
3) La batterie a apporté 180 W pendant 2h donc une énergie de E = 180 x 2 x 3600 = 1,30 MJ. Le terrain étant plat, cette énergie a permis de compenser les frottements (route, air) et ainsi éviter au cycliste de fournir un effort.
4) L'énergie consommée par les frottements correspond au "travail des forces de frottement". On note cette énergie W = F x d avec F la valeur des forces de frottement et d la distance parcourue. Donc F = 1,3 MJ / 40 km = 1,3.106 J / 40.103 m = 32,5 N
5) La batterie va servir à lutter contre les frottements mais aussi à lutter contre l'attraction de la Terre. On suppose que le cycliste fait 60kg, les frottements étant égaux à ceux calculés précédemment (approximation). Pour gagner 500 m d'altitude il faut :
Ep = m.g.h = 82 x 9,81 x 500 soit environ 400 kJ.
La batterie disposant de 1,30 MJ, il reste donc 900 kJ pour lutter contre les frottements.
On peut donc en déduire sur quelle distance la batterie pourra compenser les frottements : d = W / F = 900.103 J / 32,5 = 28.103 m = 28 km
Cette valeur est à comparer aux 40 km d'autonomie sur terrain plat. On vient de mettre en évidence l'importance du relief du parcours.
