Flux thermique par conduction
Lorsque les deux côtés d’une paroi sont à des températures différentes, l’énergie thermique passe du côté le plus "chaud" vers le côté le plus "froid".
Le flux est la puissance thermique traversant la paroi.
\boxed {\Large \phi=\frac{Q}{\Delta t}}
\phi en W
Q en J
\Deltat en s
Résistance thermique et flux
La résistance thermique d'une paroi traduit son aptitude à s'opposer au transfert thermique.
\boxed {\Large R_{TH}=\frac{T_1-T_2}{\phi}}
R_{TH} en K.W-1
\phi en W
T en K (ou °C)
Remarque :
En électricité R = U / I avec U la différence de potentiel (ce qui provoque le passage du courant) et I l'intensité (flux de charges électriques). On retrouve ici une expression similaire !
Résistance et conductivité
Conductivité thermique d'un matériau
La conductivité thermique d'un matériau traduit son aptitude à laisser passer le flux thermique. Un isolant aura donc une faible conductivité thermique. Les valeurs des conductivités thermiques des matériaux sont connues, il est facile de les trouver dans des tables, sur internet ou chez des fabricants.
Dans le tableau ci-contre on peut voir les valeurs des matériaux de construction usuels, et donc identifier les meilleurs isolants.
Conductivités thermiques de différents matériaux
Résistance thermique d'un matériau
La résistance thermique d'un matériau est liée à son épaisseur et à sa nature. Plus le matériau est isolant et épais, plus l'énergie thermique aura du mal à le traverser. Cette grandeur est très utile pour choisir un isolant car elle ne prend pas en compte la surface totale d'un mur mais est relative à 1m² d'isolant.
\boxed {\Large R_{TH}=\frac{e}{\lambda}}
R_{TH} en m2.K.W-1
e en m
\lambda en W.m-1.K-1
ATTENTION : la résistance dont on parle ici n'est pas celle qui a été définie par \Large R_{TH}=\frac{T_1-T_2}{\phi} puisqu'elle est associée à 1m² de matériau et pas à une paroi entière.
Résistance thermique d'une paroi
On retrouve ici la résistance thermique définie au tout début du cours par \Large \phi=\frac{Q}{\Delta t}. Elle concerne une paroi de surface connue.
\boxed {\Large R_{TH}=\frac{e}{\lambda \times S}}
R_{TH} en K.W-1
e en m
\lambda en W.m-1.K-1
S en m²
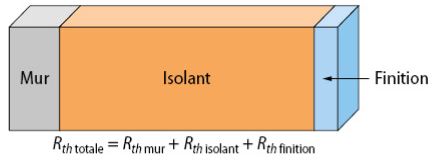
Résistance thermique d'un "sandwich" de matériaux
Quand une paroi est constituée de plusieurs matériaux, la résistance totale est la somme des résistances thermiques de chaque couche.
{\boxed {\Large R_{th}=R_{mur}+R_{isolant}+R_{finition}}}
Ci-contre un exemple de mur constitué d'un "sandwich" de matériaux.
On voit bien que l'isolation de l'ensemble est essentiellement due au PolyStyrène Expansé.
