Pression dans un fluide
Notion de pression
"Il est plus facile de marcher sur la neige fraîche avec des raquettes que sans. De même, il est plus facile d'enfoncer un clou bien pointu qu'un clou plat dans un morceau de bois. Ou encore, on préfère généralement se faire marcher sur les pieds par un grand gaillard en basket que par une jeune femme en talons aiguilles. Lorsque l'on exerce une action mécanique la simple connaissance de l'intensité de la force exercée n'est pas suffisante ; il faut également tenir compte de la surface sur laquelle s'exerce effectivement la force."
1. Pour une même force exercée sur un objet, quel paramètre modifie de façon importante son effet ?
2. Proposer une relation entre pression, force et surface d'application.
3. Rechercher sur internet les unités de pression et les appareils permettant de la mesurer.
4. Si la force s'exprime en N et la surface en m², en quelle unité s'exprime la pression ?
1. Plus la surface sur laquelle est exercée la force est faible plus la sensation de "pénétration" est grande. La surface a donc une grande influence sur l'effet de la force.
2. On peut imaginer que si on double la force la pressions double donc P est proportionnel à F. Si on double la surface la pression est divisée par 2 donc la pression est inversement proportionnelle à la surface. On en déduit une relation probable :
\Large {P=\frac{F}{S}}
3. Les différentes unités de pression sont le bar, l'atm (atmosphère), le Pa (Pascal), le mm de Hg (millimètre de mercure) et le N/m².
1 bar ≈ 1 atm ≈ 105 Pa ≈ 760 mmHg
4. Dans l'expression large {P=\frac{F}{S}} la pression est exprimée en Pa.
latex]\boxed {\Large {P=\frac{F}{S}}} avec \boxed {\Large {[Pa]=\frac{[N]}{[m^2]}}}[/latex]
Statique des fluides
On dispose d'un tube en U rempli d'eau colorée (pour bien voir les niveaux). Les deux extrémités sont laissées à l'air libre puis l'une d'entre elle est soumise à une pression (à l'aide d'une seringue) qui est mesurée à l'aide d'un pressiomètre.
1. Qu'observez-vous lorsque les deux ouverture sont à l'air libre. Proposer une explication.
2. Pour différentes valeurs de pression (une dizaine) mesurer la différence de niveau h de liquide dans les deux tubes.
3. Tracer P = f(h)
4. Déterminer l'équation de la caractéristique P = f(h).
5. Calculer le produit rho times g et le comparer à la pente de la caractéristique.
On rappelle que \rho_{eau} = 1kg.L^{-1}
6. Conclure
On obtient les mesures suivantes
h (cm) | 0 | 4 | 8 | 14 | 18 | 22 | 26 | 28 | 30 | 32 |
P (Pa) | 955 | 960 | 965 | 970 | 974 | 978 | 982 | 984 | 986 | 988 |
1. Lorsque les deux tubes sont ouverts les surfaces des liquides sont soumises à la même pression : la pression atmosphérique. Les deux liquides sont alors au même niveau.
2. On trace P=f(h) à partir des mesures réalisées et on obtient la courbe suivante.
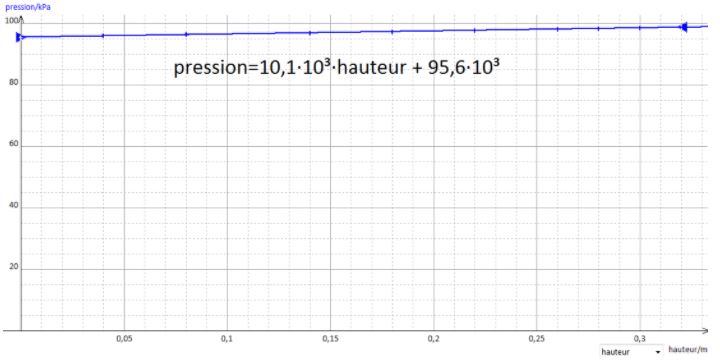
Cette courbe est une fonction affine dont on peut trouver l'équation. Pour h=0 (ordonnée à l'origine) on retrouve la pression atmosphérique d'où :
\large {P(h) = P(0) + k \times z}
On voit que la pression augmente lorsqu'on descend dans le fluide. Dans l'expression z positif voudra dire qu'on se trouve "plus bas"
On remarque que le produit \rho \times g = 10^4 est égal au coefficient directeur k de la fonction affine. La loi fondamentale de l'hydrostatique est confirmée :
\boxed {\Large {P = P_0 + \rho \times g \times h}}