La résistance thermique d'un matériau est primordiale pour réaliser l'isolation d'une habitation. On souhaite la déterminer expérimentalement.
Documents
Lien entre le flux et la résistance thermique
Le flux thermique est la puissance thermique qui traverse une paroi, du côté "chaud" vers le côté "froid".
\boxed {\Large {\phi=\frac{(\theta_{chaud}-\theta_{froid})}{R_{th}}}}
- \phi : flux thermique en W
- R_{th} : résistance thermique du matériau en K.W-1
- \theta_{chaud} et \theta_{froid} : températures de part et d'autre de la paroi (en °C ou en K)

Conductivité thermique d'un matériau
La conductivité thermique est une grandeur physique qui caractérise la capacité des matériaux à conduire la chaleur. Elle est liée à la résistance thermique d'une paroi et à son épaisseur
\boxed {\Large {\lambda=\frac{e_{paroi}}{R_{th} \times S}}}
Mesurer une résistance thermique
Sans appareil spécifique
Pour mesurer la résistance thermique d'un matériau on place ce dernier entre deux sources de chaleur de températures constantes :
- Source chaude : vapeur d'eau (100°C)
- Source froide : glace fondante (0°C)
L'énergie thermique va alors "traverser" le matériau du côté chaud vers le côté froid.
Afin de mesurer le flux thermique, on va mesurer le temps nécessaire pour la faire fondre une masse connue de glace. La connaissance de la chaleur latente de fusion de la glace (333 J/g) nous permettra de connaître l'énergie ayant traversé le matériau et ainsi en déduire le flux thermique.
\boxed {\Large {\phi=\frac{(\theta_{chaud}-\theta_{froid})}{R_{th}}}}

Avec un appareil spécifique
Cet appareil est constitué d'une résistance (point chaud de température constante) sur laquelle est disposé un échantillon du matériau à étudier. Sur l'autre face du matériau se trouve une autre plaque dont la température est mesurée (point froid).
La tension et l'intensité traversant la résistance sont connues, et on observe la variation de température de la plaque "froide". Lorsque le régime permanent est atteint (la température de la plaque froide n'évolue plus) le flux thermique est égal à la puissance électrique de la résistance.

Mesures de la résistance thermique des matériaux
Sans appareil spécifique
Faire bouillir l'eau du bécher "source chaude" en plaçant au dessus le matériau.
Au bout de quelques minutes on considère que le régiment permanent est atteint et on place que dessus du matériau le bécher (rempli au tiers) contenant la glace fondante. On déclenche le chronomètre et, tout en agitant la glace, on mesure combien de temps est nécessaire pour faire fondre toute la glace.
Questions :
- Calculer l'énergie reçue par la glace pour fondre
- En déduire le flux thermique traversant le matériau
- Calculer la résistance thermique du matériau
- En déduire la conductivité du matériau et la comparer à la valeur théorique
Pour l'exemple nous prenons comme matériau un morceau de bois d'épaisseur 5mm.
Énergie reçue par la glace
On a placé 88g de glace fondante (0°C) dans le bécher.
Au bout de 9 minutes 30 s (soit 570s) on retire l'eau issue de la fonte de la glace et on mesure une masse de glace restante de 9g.
On en déduit que 79 g de glace a fondu, ce qui nous permet de calculer l'énergie reçue par la glace.
Si on place à nouveau 88g de glace dans un bécher et qu'on le laisse à l'air libre, une partie de la glace va fondre en prenant de l'énergie de la salle de classe. On mesure la masse de glace qui fond "naturellement" en 9 minutes 30 s et on trouve 23,6g.
Le chauffage a donc réellement fait fondre 55,4g de glace !
Énergie ayant traversé le matériau :
Q = m x Lf = 55,4 x 333 = 18,5 kJ
Flux thermique à travers le matériau
Il est égal au quotient de l'énergie par le temps de fonte :
\phi=\frac{Q}{\Delta t}=\frac{18,5.10^3}{570}=32W
Résistance thermique du matériau
R_{TH}=\frac{(\theta_{chaud}-\theta_{froid})}{\phi}=\frac{100}{32}=3,1K.W^{-1}
Conductivité thermique du matériau
R_{th}=\frac{e}{S \times \lambda} donc \lambda=\frac{e}{S \times R_{th}}=\frac{0,005}{\pi \times R^2 \times R_{TH}}=0,30 W.°C^{-1}.m^{-1}
Les tables donnent une valeur de l'ordre de 0,14.
La valeur que nous trouvons est très éloignée de la valeur théorique ( de l'ordre de 100%). Il faudrait prendre en compte qu'une partie de l'énergie sert à chauffer le matériau, que le matériau perd régulièrement de l'énergie lors du chauffage, que de la vapeur d'eau vient se liquéfier sur les parois du bécher etc. Notre montage nécessite donc de grandes améliorations.
Avec appareil spécifique
Observer les mesures réalisée avec l'appareil dédié.
Réaliser une synthèse orale expliquant ce qu'on observe et les résultats obtenus.
On place ici un échantillon de matériau d'épaisseur et de dimensions connues entre les deux plaques de l'appareil de mesure.
Une fois le régime permanent atteint on peut dire que la puissance de chauffage compense exactement le flux thermique à travers le matériau (puisque la température du point "froid" ne change plus).
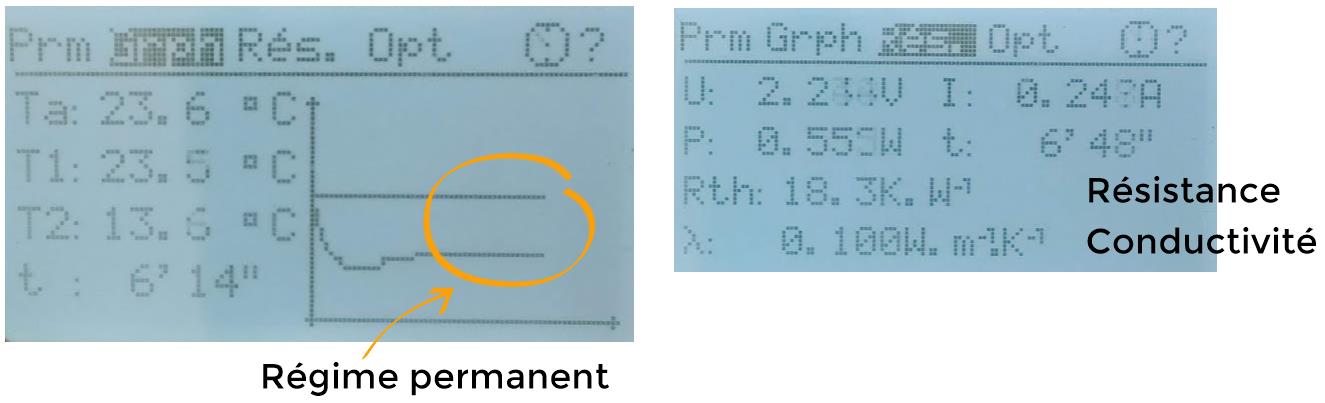
Le flux est donc égal à la puissance électrique, c'est à dire UxI.
L'appareil calcule alors pour nous directement la résistance thermique et la conductivité.
