Rappels de première
Référentiel, repère, position d'un point, trajectoire.
Caractéristiques du mouvement d'un point
Vecteur vitesse
Variation du vecteur vitesse et sa construction
Dérivée et primitive d'une fonction
Système - Référentiel - Repère
Avant toute étude je dois définir :
- Système : c'est ce dont on veut étudier le mouvement. En terminale on l'assimilera à un point, son centre de gravité (pour simplifier l'étude).
- Référentiel : c'est l'objet par rapport auquel on va étudier le mouvement.
- Repère : c'est lui qui nous permet de repérer l'objet, par sa position et la date à laquelle il s'y trouve que l'ont notera M(t)
Position \overrightarrow{OM}(t)
La position d'un objet est définie par ses coordonnées et la date.
Pour la suite on aura besoin du vecteur position : \overrightarrow{OM}(t) = \dbinom{x(t)}{y(t)}
Remarque :
Pour simplifier les écritures, comme on sait que x et y dépendent du temps on n'écrira plus x(t) et y(t) mais x et y d'où : \boxed {\overrightarrow{OM} = \dbinom{x}{y}}
Pour la suite je fais le choix de ne plus noter x(t), V(t) ou a(t) mais x, V et a afin de clarifier les écritures.
Vitesse \overrightarrow{V}(t)
Le vecteur vitesse est défini comme la dérivée du vecteur position :
\boxed{\overrightarrow{V} = \frac{d\overrightarrow{OM}}{dt} = \dbinom{ \frac {dx}{dt}} {\frac{dy}{dt}}}
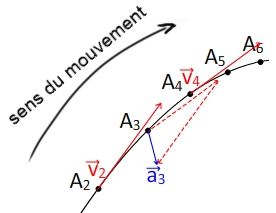
Pour tracer le vecteur vitesse plusieurs méthodes sont possibles, mais ce ne sont que des méthodes approximatives ! La méthode qui donnera le meilleur résultat est la méthode du point milieu qui consiste à tracer la vitesse moyenne entre le point d'avant et le point d'après.
Accélération \overrightarrow{a}(t)
Le vecteur accélération est défini comme la dérivée du vecteur vitesse : \boxed{\overrightarrow{a} = \frac{d\overrightarrow{V}}{dt} = \dbinom{ \frac {dV_x}{dt}} {\frac{dV_y}{dt}} = \dbinom{ \frac {d^2x}{dt}} {\frac{d^2y}{dt}}}
L'accélération est donc la dérivée seconde de la position.
Comme pour la vitesse, la méthode graphique "la plus juste" est celle du point milieu :
\boxed{ \overrightarrow{a_3} = \frac{\overrightarrow{V_4}-\overrightarrow{V_2}}{t_4-t_2}}
Mouvements circulaires
Définition du repère
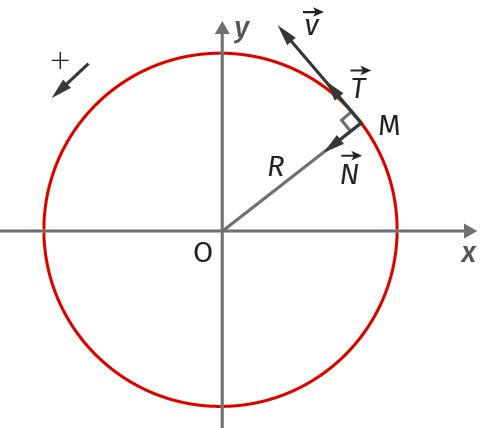
Pour les mouvements circulaires il est bien plus facile de travailler dans un repère tournant appelé repère de Frenet.
Ce repère sera centré sur le point étudié et aura comme vecteurs unitaires :
- \overrightarrow{T}, vecteur porté par la tangente à la trajectoire et dans le sens du déplacement
- \overrightarrow{N}, vecteur normal à la tangente (perpendiculaire) dirigé vers le centre de la trajectoire
Pour les mouvements circulaires il est bien plus facile dDans ces conditions les vecteurs poisition, vitesse et accélération s'exprimeront :
- Position : \boxed {\overrightarrow{OM} = - R \times \overrightarrow{N}}
- Vitesse : \boxed {\overrightarrow{V} = V \times \overrightarrow{T}}
- Accélération : \boxed {\overrightarrow{a} = \frac{dV}{dt} \times \overrightarrow{T} + \frac{V^2}{R} \times \overrightarrow{N}}e travailler dans un repère tournant appelé repère de Frenet.
On ne confondra pas la dérivée du vecteur vitesse et la dérivée de la valeur de la vitesse (sa norme).
\boxed {\frac{d\overrightarrow{V}}{dt} \ne \frac{dV}{dt}}Cas du mouvement uniforme
Dans le cas d'un mouvement uniforme la norme de la vitesse serait constante, sa dérivée sera donc nulle d'où :
\frac{dV}{dt} \Leftrightarrow \boxed{\overrightarrow{a} = \frac{V^2}{R} \times \overrightarrow{N}}On voit que dans ce cas l'accélération est centripète (dirigée vers le centre du cercle) et si on applique la seconde loi de Newton on peut conclure que la somme des forces qui s'appliquent au système est elle aussi centripète.
C'est le cas par exemple des planète qui ont une trajectoire circulaire uniforme, on peut en déduire qu'elles ne sont attirées que pas un astre.
Pour aller plus loin : vers le supérieur
La vidéo ci-contre est une démonstration des coordonnées du vecteur accélération dans le repère de Frenet. Intéressant pour les élèves qui souhaitent viser une école d'ingénieur dans le futur ou des études clairement scientifiques.